Symmetrical components is a subject that makes most engineers wince in pain and frustration when they first hear these words.
Before the days of computer-assisted fault current calculations, all fault calculations were done by hand.
In the modern world, short circuit calculations are completed with the help of computer simulated calculations, however, the NCEES® Electrical Power PE Exam still tests on the basic understanding of symmetrical components for unbalanced faults, and for good reason.
It’s important to understand how each type of unbalanced fault has an effect on the actual available short circuit current at any point in an electrical system.
Below is a realistic NCEES® like practice problem demonstrating how to calculate the short circuit current for an unbalanced single line to ground fault using symmetrical components.
What’s in this article? – Single Line to Ground Fault Symmetrical Components
Click below to jump to any section.
1. NCEES® Electrical Power PE Exam Practice Problem – Single Line to Ground Fault
2. Example Problem Demonstration Video
3. Single Line to Ground Fault Single Phase Equivalent Circuit
4. Solve for the Per Unit Current in the Single Line to Ground Fault Circuit
5. Calculate the Base Current
6. Calculate the Current in Amps
7. Calculate the Single Line to Ground Fault Current
8. Need More Practice?
9.Thoughts? Comments? Questions?
1. NCEES® Electrical Power PE Exam Practice Problem – Single Line to Ground Fault
Please note: this is a practice problem created by the authors at Electrical PE Review, INC to simulate a realistic PE exam practice problem, it is not an official practice problem from NCEES®.
Symmetrical Components Single Line to Ground Fault Example Problem:
A single line to ground fault occurs somewhere along the 50 mile transmission line connecting the utility substation bus #1 to transmission bus A. Using the transmission line diagram, solve for the fault current magnitude in amps at this point if the zero sequence impedance is 0.241pu, and the positive and negative sequence impedances are both equal to five times the zero sequence impedance. Use the generator power rating and the system voltage at the fault as base values.
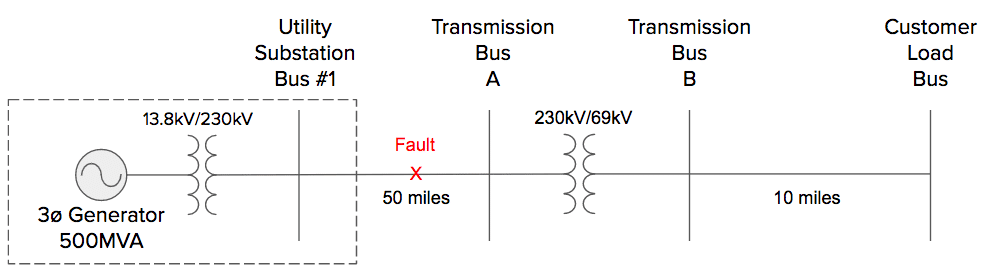
(Transmission Line Diagram)
2. Example Problem Demonstration Video
Follow along step by step by watching the above practice problem worked out live with the symmetrical component single line to ground fault video:
3. Single Line to Ground Fault Single Phase Equivalent Circuit
The first step is to draw the single-phase equivalent circuit for the single line to ground fault using symmetrical components. Then plug in the values given in the problem. Each type of fault has its own unique symmetrical component circuit so be sure to have a reference handy.
A single line to ground fault has all three sequence networks – zero, positive, and negative – connected in series:
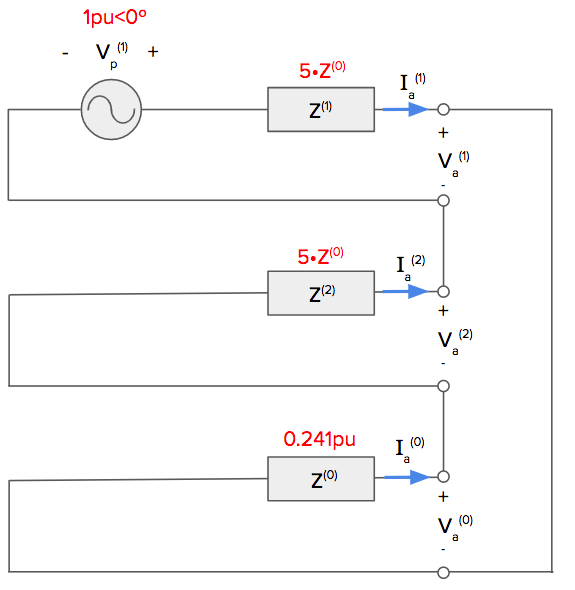
(Single Line to Ground Fault Symmetrical Components Single Phase Equivalent Circuit)
We use 1pu<0 as the per unit value of the phase voltage in the equivalent circuit. If you’re unsure why, or rusty with the per unit system, the following article may help explain why:
Electrical PE Review – Per Unit Example, Tips, and Tricks
4. Solve for the Per Unit Current in the Single Line to Ground Fault Circuit
From circuit analysis, we can determine that Ia0, Ia1, and Ia2 are equal to each other since they are in series:
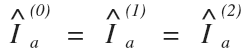
Let’s use ohm’s law to solve for the current by adding all three series impedances together:
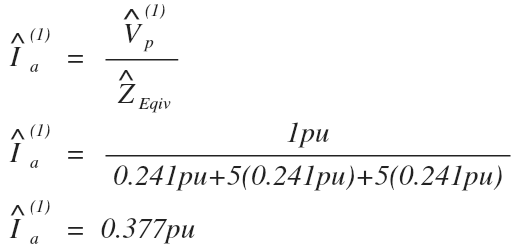
The per unit current in the single line to ground fault single-phase equivalent circuit is 0.377pu.
5. Calculate the Base Current
We know the value of the current in per unit, but the question specifically asks for the current in amps.
To convert from per unit to amps, we will need to first calculate the base current.
We will use the power rating of the generator for base power and the system voltage for base voltage, as instructed by the problem statement.
Don’t forget, since this is really just the formula for the magnitude of three phase power, we’ll need to use the line voltage value for the base voltage value, and don’t forget the square root of three.
Confused as to why we used this formula? The following article may help to explain why:
Electrical PE Review – The Three Most Common Mistakes to Avoid for Power Formulas
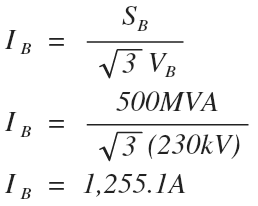
The base current is equal to 1,255.1 amps.
6. Calculate the Current in Amps
Now that we know both the per unit and base values of the current, it’s time to calculate it in amps using the per unit system:
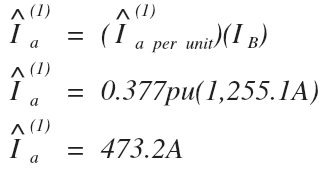
The current in the single line to ground fault single-phase equivalent circuit is 473.2 Amps.
7. Calculate the Single Line to Ground Fault Current
For a single line to ground fault, the current flowing through the fault will only be from the phase that is faulted. Assuming the fault occurred on the A phase, this means the fault current will equal the A line current at the time of the fault.
Or we can say that I_F = I_A:
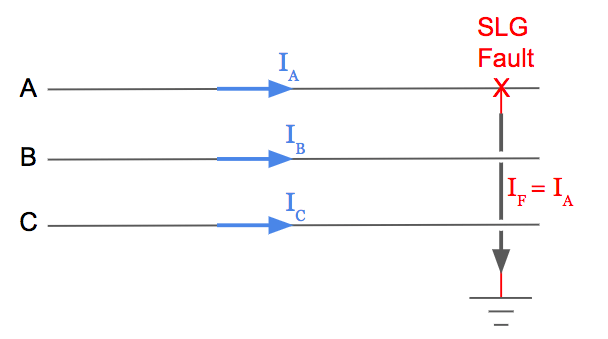
(Single Line to Ground Fault on A Phase – Three Phase Diagram)
Next, since this is a three phase transmission system, the line current in the system will equal the phase current in the single phase equivalent circuit (think of wye : wye relationships where I_phase = I_Line).
That means we will need to use the symmetrical components formula that calculates the A phase current from the sequence currents:
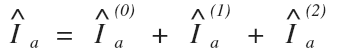
Since we already demonstrated that the positive (1), negative (2), and zero (0) sequence currents are all equal in a single line to ground fault, we can solve for the A line current using the value we calculated for Iao in the previous step:
Since:
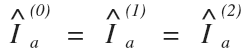
Then:
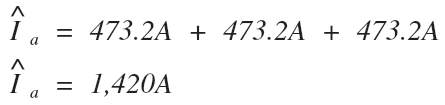
The A line current in the transmission system during the single line to ground fault is 1,420A(rounded to the nearest amp).
Since we demonstrated that the fault current will equal the line current for a single line to ground fault, we can solve for the fault current:
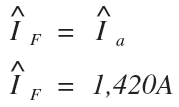
The fault current is equal to 1,420 amps (rounded to the nearest amp) in the single line fault for the transmission system in the given problem.
That wasn’t so bad, was it?
Okay, maybe it was a little challenging if this was your first time working this type of problem. It get’s easier with practice, I promise.
8. Need More Practice?
Make sure to watch the video embedded at the top of this article.
The video demonstration takes the single line to ground fault example one step further by demonstrating how to prove that the voltage on line that is faulted is equal to zero – (assuming it is a zero impedance fault) – by calculating the A phase voltage from the sum of the positive (1), negative (2), and zero (0) sequence voltages.
Want to try it on your own?
First, you’ll need to calculate the positive (1), negative (2), and zero (0) sequence voltages.
If you are already a student of ours, you can go directly to the chapter on symmetrical components that offers video demonstrations of each type of fault by clicking the following link (you must log in):
Electrical PE Review – Chapter 4.2 Symmetrical Components
You can also work the practice problem quiz that features 10 sample PE exam problems with full worked out solutions, similar to this article:
Electrical PE Review – Chapter 4.2 Quiz! Symmetrical Components
9. Thoughts? Comments? Questions?
Have you ever come across a tough symmetrical components question that you couldn’t answer?
Is this the first time you’ve seen a full-length explanation on solving a single line to ground fault?
Have any lingering questions after working your way to the bottom of this article?
Join the discussion by leaving your comment below.
We respond to all comments in a timely manner.

Excellent article Zach. This was very helpful!
Glad you enjoyed it, Justin.
Zach ………………….. do you have a book to accompany the course that can be used during the exam?
Dave
Hi David,
Yes. For more information please visit our frequently asked question page there is more information on how to use the course material as exam reference: electricalpereview.com/frequently-asked-questions-faq/
Zach,
What happens to the voltage sequence in the equation?
Isn’t the equation Va(0)=Vp- Za(0)*Ia(0) (considering zero sequence as an example).
Hi Bhaskar,
That equation is not valid for a single line to ground fault, which is why using each of the specific circuits for each type of fault is so important. The relationships need to be derived off each individual single phase equivalent circuit.
For a single line to ground fault:
Va(0) = -Ia(0)Za(0)
Hi Zach,
Thank you for reply. I am a little confused. In the NCEES practice problem #514 they specify a phase to ground fault and to find sequence voltage they use
Va1=Vp- Ia1*Z1 in their solution.
Zach, I was actually asking about the positive sequence voltage Va1=Vp- Ia1*Z1 . When we calculate Ia1 we do not use Va1 and we use Ia1= Vp/Zeq. Why do we not consider the Va1 from Va1=Vp- Ia1*Z1 then?
Hi Bhaskar,
You absolutely could use the second formula to solve for Ia1 if you knew the value of Va1 but Va1 is not given so we would have to calculate it first, hence the first equation.
This is one of the topics I’ve struggled with the most while studying but this article has made it much clearer to me. Thank you!
This article as well as the symmetrical components module was really helpful. I appreciate how you break down each step with a simple and clear explanation.
Most text books don’t go to the depth in understanding of Symmetrical components that you have shown in the article and your modules on the topic. Your single phase equivalent circuits for each fault type I have found to be the most intuitive when determining the equations to calculate each component. I read chapters of different resources but it was your videos and teachings that really brought the concept home for me. Thanks Zach!
This example, combined with the associated video, really helped me understand symmetrical component analysis. I was able to use what I learned in this article to solve a practice problem on the official NCEES practice exam, so I feel pretty good about solving similar problems going into the actual exam.
This is a hard topic I have struggled with but this example has clarified a few things for me and I can now say I feel more comfortable dealing with this type of problems.
Great explanation!
Thanks EJ, glad you enjoyed it.
very useful to have a working example of 2 subjects i struggle with.
Broadens my understanding on this topic!
This is great stuff. For sure, I’ll print this out to use as a reference during the exam.
Helped me solve a practice test question. Know I’ll solve it on the real test now!
Symmetrical components is a small, but important topic in the PE exam. Thank you Zach for your clear instructions. I am definitely going to work this out multiple times and take this to the PE exam.
hey Zach
I enjoyed this article. The techniques that you use to demonstrate symmetrical components make this complicate subject easier to understand.
excellent article. I just went through it. I don’t think i had seen this one before. ahh symmetrical components, i must say this article helped a better understanding of the topic. The module has also helped alot.
thanks Zach
Very useful. Thanks Zach
These symmetrical component problems are such a pain. I had to re-read this article a couple times and watch the videos before I finally got it. I could have never understood fully if I was just reading these in a book, so thanks Zach, this really helps.
Symmetrical component use to scare me, but not any more after going through this article couple of times. You make it so easy to understand.
this article was helpful in walking through step by step on how to solve a difficult problem. This will be a great reference for other similar problems.
I find this article in symmetrical components to be extremely helpful to me since I never had the opportunity to learn this. This is a well designed article and would recommend that others would read through it to gain a better understanding of this concept. Thank you for a job well done Zach!
Symmetrical components is one of those topics that you either find them very poorlyexplained on different materials out there or some books go too deep, making you loose time when you are in a tight schedule like preparing yourself for the PE exam. Zach gives you the right level of information that you will need to beat the exam. I will update my post once I take it, but for now I can say I feel way more prepare than 3 months ago. Thanks!
Really great article. Single line to ground fault is the most common fault yet it’s most difficult to understand. Thanks to Zach for such an easy explanation of this difficult topic.
Positive, negative and zero sequence concept in the single phase to ground fault became very clear in my mind. Zach makes it look so easy very effective techniques in teaching the scary subject -Electrical Power Systems-after looking at phase diagrams and one line diagrams finally sink in!
Excellent Article. I believe trying not to over think symmetrical components and keep it simple is the best way to go while preparing for the test.
Thank you for explanation Zach! This was really easy to follow and now I don’t think I’ll be afraid of a symmetrical component problem on the exam.
Great article on demystifying Single line to ground fault. It clarified how a fault is compromise of symmetrical components.
Very appreciative of your module on Symmetrical Components. I fell really confident I can answer them all correctly on the exam.
This article was very helpful because it helped me learn more about Single Line to Ground Circuits and how they work.
Thanks for the information in this Article. This is a subject that I struggled in school years ago, and this article makes it very simple. I feel like I finally get ‘per unit’.
The Electrical PE Review course is the best course I have taken. The was Zach explains this material is great. He covers step by step details that make any subject easy.
The Electrical PE Review course is the best course I have taken. The way Zach explains this material its great. He covers step by step details that make any subject easy.
This explanation has been the most helpful from all that I’ve come across. Not the easiest of topics but you did great at explaining! Thanks!
This definitely helped me so much with Line-Gnd faults, especially breaking it down step by step. The hardest part was defining each variable for each type of fault.
This is one of my favorite articles. If your reading this, make sure to print this article and bring it with you to your PE exam
that’s my fav article.
it explains the fault type very clearer.
The diagrams, video and clear writing are very helpful! I even copied the examples from the video and put the notes in my reference. While I’ve seen these diagrams and formulas in other books it didn’t click because I was missing that final push to bring it home. The videos with worked problems with explanations on WHY we’re doing things (along with qualitative points too) are the quintessential piece!
These symmetrical component problems can be weird. Books make Symmetrical Components looks like a combination of Maxwell’s equations coupled with a little Black Magic. With Zach’s instruction it finally started making sense. Thanks Zack — this really helps.
Very well explained. Could not find a better article than this anywhere. Thank you Zach !
Hi Zach,
This is very helpful. I don’t deal this in my field but understand how symmetrical components works especially in fault current.
Thank you.
This article and the examples from the video are absolute must-haves in your PE reference material. Really de-mystifies the concept of symmetrical components!
By far the most concise and complete explanation I have experienced. Thank you Zach!
Great explanation Zach! Symmetrical components is one of the most complicated topic that a Power Systems Engineer need to understand. Your explanation to this article gave me much more clarity on this topic. Thank you Zach!
This article and the video on youtube helped me know the topic really good.
I feel I am ready now to solve any questions. I added this to my materials that I will take to the exam.
Good job Zach in making this article available for PE exam candidate. I never like symmetrical components because I found them difficult but now I am no longer afraid. I will definitely print this article for the exam.
Symmetrical components is impossible to understand in all of my other reference materials. I’m so glad for this article! The step by step detailed solution is extremely helpful and beneficial. Thanks Zach!
This topic was previously just a bunch of equations, now I understand where the a multipliers come from and how to answer qualitative questions as well!
I’m curious about using the sqrt 3 in to solve for the line voltage at the end of the video. Aren’t transmission lines typically delta configuration so Vp = VL ? Or is it cause of the fault to ground you now introduce a VLN that you have to solve for and that would be your fault voltage? Just wanted to confirm