Did you know that one of the most common reasons to get a question wrong even when you’ve done all the right steps is by making a mistake on the units?
I bet that sounds familiar.
Have you ever worked a problem that had all sorts of different units and you either entered it into your calculator wrong or misinterpreted the units of the answer that the calculator gave you?
What about when you are solving a problem and all the possible answer choices are the same value but in all different units:
a) 10V
b) 1kV
c) 10kV
d) 1MV
We are going to make sure we never get an answer wrong because of using the wrong units, ever again!
After all, every single point on the Electrical PE Exam counts towards a passing score.
So let’s say you’re working a fault current problem and utilizing the KVA method.
You have an upstream generator with a fault power contribution of 3,000 MVA feeding a transformer with a fault power contribution of 820.9 MVA. You want to find the fault power downstream of the transformer so you add them in parallel like this:
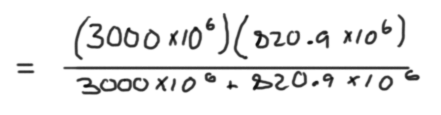
Using powers of ten for the MVA units above, or using a whole bunch of zeros on our calculator like this:
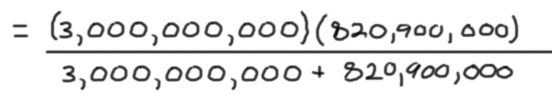
Both give the answer in the correct number of zeros or correct power of ten for the units the answer is in when you hit enter:
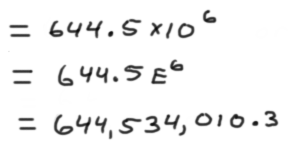
Depending on how you calculator is set up, it will show the answer in any of the three ways above.
Now, for the good stuff.
I want you to know there is a better way.
These MVA values are already quite large so entering them in the calculator using scientific notation or with a bunch of zeros is time-consuming.
It also introduces additional steps where a mistake could be made.
Instead, I want you to:
- Look at how the units will cancel each other out
- Know what kind of units the answer will be in BEFORE you solve the problem
- Enter in the least amount of numbers in the calculator as possible
These steps all contribute to reducing the chance of making any costly entry mistakes that gets us all from time to time.
So how do we do this?
The method works like this.
First, let’s work the problem using ONLY the units.
Here is the same reciprocal of sums method again for adding our two Apparent Power fault contributions in parallel, using only the units:
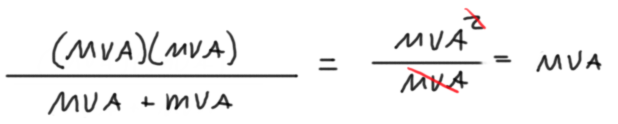
This tells us the answer will be in MVA’s. So we write down the units for the answer before we even know what the value is.
This way we don’t forget it and it prevents us from making a mistake, like this:

Next, we enter in the calculator the numbers ONLY without using powers of ten or extra zeros for the units and hit enter. Getting the answer without the correct number of decimal places, like this:
This gives us the answer without the correct number of decimal places for the units.
Here is the same example as above, this time using the MVA values of the fault contributions:
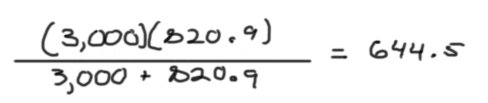
Then we write down the answer from our calculator into the spot we already have on our paper waiting for it, like this:

Bingo.
This way may seem longer at first, but I promise not only will you save precious time for each equation using this method, but it is also a great way to check your work when you need to double check if the units of your answer are correct.
It saves time on each question that can be applied toward the end of the exam to spend on harder to answer questions that require using your reference books.
It’s great.
Another point to consider is that after you do this a couple of times you will instinctively know the correct answer of your units, skipping the step of physically writing them down to see how they cancel out, and jumping straight to entering in the least amount of numbers for each value in your calculator.
It really does save you time and prevent mistakes.
How else can we use this trick?
Let’s take a look at other electrical formulas where we have a mix of units or large decimal places and are interested in entering the least amount of numbers into the calculator to save time and cut down on additional steps that may lead to simple mistakes.
For example, let’s say we are calculating the magnitude of impedance from voltage and power:
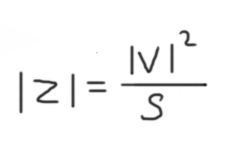
If your voltage is in kV and your power is in kVA, what units will your impedance be?
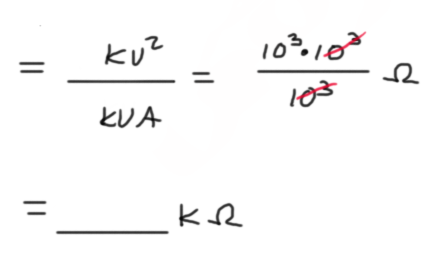
Kilo Ohms!
Getting the hang of it now?
What about the units of line current in a three system with an apparent power in MVA and line voltage in kV?
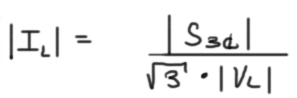
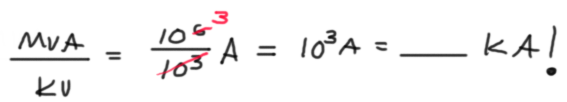
Kilo-amps!
The possibilities are endless, and you can apply this to just about every single example problem while you study and more importantly on the actual PE exam.
Thoughts? Further Questions? Examples of when you have used this successfully?
Share Below!

I really like Calculator Shortcuts and Tricks for Working with Units Quickly. These tricks helps me to do my calculation faster, easier and save time. I used to make a mistake when I tried to calculate parallel complex impedance. Now i know how to do it right with calculator.
Thank you so much.
Ray Shah
Glad it helps
Good example of efficiency. I think I’ve done this a little bit but did not apply it very often. Good to pay attention when it can be used more and WRITING DOWN THE UNITS first.
Zach, for the first example why is it said the source and transformer are in parallel?
Further down at the gigaohm example there is a “three”. But I think it’s supposed to be three-phase.
Hi Nowell,
“Good example of efficiency. I think I’ve done this a little bit but did not apply it very often. Good to pay attention when it can be used more and WRITING DOWN THE UNITS first.”
You would be amazed at how many questions via email I receive for help that end up just being an error to due units, or a negative or plus sign that did not get carried throughout the entire formula (like current conjugates and negative angles).
Try to practice writing down the units AND double checking negative and positive signs in your handwritten notes, these are easy low hanging fruit that can quickly increase your overall exam score with a minimal amount of effort. It just requires a bit of practice to make the new habit automatic.
“Zach, for the first example why is it said the source and transformer are in parallel?”
The 150MVA generator and 55MVA Transformer are in series.
However, the MVA method for solving fault current analysis problems adds up the individual MVA contributions in parallel. (Try solving this problem using the per unit method by adding up the impedances in series and you will get the same answer).
Review the fault current analysis course module for more information, I believe it is part of the free trial: https://courses.electricalpereview.com/courses/take/electrical-power-review-course/texts/1006207-5-fault-current-analysis
Since adding in parallel relies on the reciprocal of sums method, it worked out as a good example to use for this particular “units/calculator trick” to demonstrate this article’s example.
“Further down at the gigaohm example there is a “three”. But I think it’s supposed to be three-phase.”
After reviewing the article, I’m not quite sure I’m finding what you are referring to. The closest is the very last example of finding Line current using Apparent Power and Line voltage.
The units work out so that there is a ten to the power of 6 divided by a ten to the power of 3. If you are referring to the red power or 3 next to the stricken through black power of 6, then that red power of three is just demonstrating that a ten to the power of 6 divided by a ten by the power of 3 will equal a ten to the power of 3.
If that’s not it feel free to clarify further. Not being able to insert images in blog article comments can sometimes make it harder to have more in-depth discussions.
During my first month of studying, I focused on mastering my calculator. This article and some YouTube videos helped me to learn how to be more efficient in solving problems, so I don’t waste valuable time trying to figure out how to use the calculator during test day. thanks for the tips!
i always keep forgetting write the units and sometimes without it I missed where kilo or mega, but after your videos now i always write my units and now i was able to calculate with calculator sometimes not even type all number, skip kilo or mega, because i can see what my answer will be.
Thanks a lot! Its helps me reducing my calculations and save time.
Glad it helped Rajat!
Excellent article. I like the tip on checking the units of the answer before solving the problem as well as how the units will cancel each other out.
Can’t explain how many times using the correct units has burned me in my studies. This module is great for helping you just slow down and realize what is being asked.
I would really recommend reading through this article, any time you can save on the exam is gold. Time you can spend on other problems. Master these tricks and you will be good to go.
Generally I do not comment on blogs but your article is so convinced that I have never stopped myself to say something about it. You’re a great man, continue it.
Great Article, Learning how to quickly and efficiently use your calculator is extremely important. Personally, I use the TI-36X Pro, and I love the fraction button above the 7 button. Helps avoid so many mistakes.
Calculator shortcuts and understanding units are worth mastering. We can’t let ourselves get questions wrong on the PE Exam because of this.
This is one of those articles I reviewed because it was part of the syllabus of the class, and I figured I would skim through it. Once I started applying these concepts to my practice problems, I realized I wasn’t mis-typing things into my calculator as often, and had higher accuracy and more speed. Thanks for kicking my butt, Zach!
Might be silly but this was really helpful. Letting the calculator do all the heavy work is the best thing.
Excellent article! If you’re still checking the comments on this one, here’s a typo check.
Right after the first equations…
“Depending on how you calculator is step up, it will show the answer in any of the three ways above.”
Should say “calculator is set up” and not “step up”
“Enter in the less amount of numbers in the calculator as possible”
Grammar error, “less” should be “least”
“Next, we enter in the calculator the numbers ONLY without using powers of ten or extra zeros for the units and hit enter. getting the answer without the correct number of decimal places, like this:”
Should capitalize “Getting” in the second sentence.
“Then we write down the answer from out calculator into the spot we already have on our paper waiting for it, like this:”
Should say “our calculator” and not “out”
“let’s take a look at other electrical formulas where we have a mix of units or large decimal places and are interested in entering the…”
Should capitalize “Let’s take a look…”
And lastly should probably put a space in between “KiloAmps!” to be consistent with the previous problem.
Thanks again Josh! These have all been corrected.
This was a great practical tip. I was following along, punching in numbers long form and made a mistake in doing so. But I didn’t with the simplified method. Thanks.